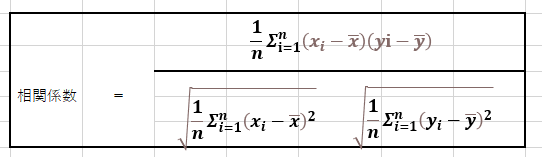
回帰分析の中でもシンプルな手法である単回帰分析
例えば、部屋の広さと家賃といった2つの変数の関係性を表す指標が相関係数である。
この関係性を表す式を求めるのが回帰分析である。
さらに扱う変数を増やした重回帰分析がある。
家賃、広さ、役からの距離、築年数、設備など複数の要素が絡み合っている。
重回帰分析を使えば、複数要素の影響を知ることができる。
3.1 回帰分析とは
回帰分析とは、ある変数xが大きくなる場合に、別の変数yにどの程度の影響を与えるのかを測定する手法である。
回帰分析では、2つの変数間の直線的な関係を前提とする。
直線的な関係は、その関係性を測る指標である相関係数のこと。
変数間の相関関係を式に表したものを回帰式と呼ぶ。
一方の変数を原因、もう一方を結果と呼ぶ。
変数xを説明変数(独立変数)、説明される変数yを目的変数(または、被説明変数、従属変数)と呼ぶ。
回帰分析は、2つ変数の散布図を描いた場合、その散らばり具合を最もうまく表す、一番当てはまりの良い直線を引くのが最もシンプルな図となる。
3.2 単回帰分析
単回帰分析は、ある1つの説明変数xが大きくなる場合、別の目的変数yにどの程度の影響を与えるのかを測定する。
その測定ができると、ある1つの説明変数xを用いて、別の目的変数yを予測できるようになる。
回帰分析では、説明する変数xと説明される変数yを明確に区別し、認定する必要がある。
3.2.1 単回帰分析のステップ
単回帰分析の手順は下記の通りである。
(1) 説明変数と目的変数を決める
(2) データの特徴確認と散布図の描画
(3) 回帰式を求める
(4) 回帰式の精度を確認する
(5) 予測する
(1) 説明変数と目的変数を決める
何を推定したいのか?で、目的変数を決める。
何を使って推定するのか?で、説明変数を決める。

目的変数は、回帰分析の目的、もしくは、業務上のニーズから決めることがほとんどである。
説明変数は、仮設を考えて決める必要があり、難しい。
(2) データの特徴確認と散布図の描画
対象のデータが正規分布に従うか、確認が必要。
完全に従うということはないが、正規分布に従っているという前提で分析を進める事が多い。
必ず、説明変数と目的変数の散布図を描いて、2つの変数間の相関係数を求め、データ間の関係を掴むようにすること。
1つの特異値によって、相関係数が高くなり、正しい結果を得られない可能性もある。
また、相関係数が低くても、変数間に直線的ではない関係があることも多い。
散布図をみて、変数が傾向なくばらついており、相関係数も低い場合、回帰分析では良い結果を得られない可能性が高い。
(3) 回帰式を求める
2つの変数は、1次式の関係にあると言える。
1次式は、回帰式となる。
単回帰分析において、求めるべき回帰式は、下記の通り。
y=ax+b
この回帰式でyが目的変数、xが説明変数、aが回帰係数、bを切片と呼ぶ。
単回帰分析における回帰式は、直線と成る。
傾きがa回帰係数、y軸と交わる点のy座標の値がb切片となる。
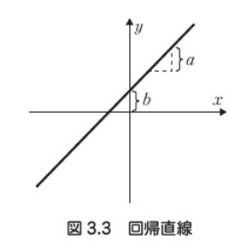
回帰式の見た目は、aとbによって、決まる。よって、aとbを調整し、回帰式をデータにフィットさせることで
適切な回帰式を求める。
aとbというパラメータの最適値を求めるプロセスを最適化と呼ぶ。
最適化の最もよく使われる手法は、最小二乗法である。
① 最小二乗法
2つの変数の関係を示す当てはまりの良い線を引くのが回帰分析である。
2つの変数の関係を最も良い当てはまりのよい線を探し出す手法が、最小二乗法である。
回帰直線を求められると、説明変数から目的変数を予測すことができる。
求めたい直線=最も当てはまりの良い線となり、説明変数から最もうまく目的変数を予測できる直線である。
この最適な線は、回帰直線を用いた予測値と実績値の差が小さい時と言える。
予測値と実績値の差をコスト、または、残差と呼ぶ。
これが最小となる直線である。
残差を単純合算しても、正しく求められない。予測値は実績値より大小さまざまになるため。
よって、残差を二乗し、符号をすべて正に統一した上で総和を求め、これの最小化を目指す。
この手法が最小二乗法である。
② 最小二乗法の数学的な理解
残差(コスト)の二乗の総和は、下記の式で表すことができる。

③ Excelを用いた回帰式の算出
Excelには、説明変数と目的変数のデータから回帰式を未知軸関数がある。
その機能を使うためには、アドインによって、分析ツールをインストールする必要がある。
※巻頭のExcel分析ツールのインストールについて、手順を参考にインストールすること。
サンプルデータ5を使用。
(a) 近似直線を追加する方法

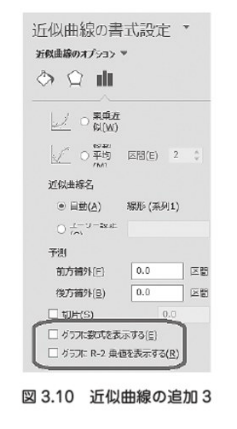

直線を右クリックして、近似直線の書式設定を押して、グラフに数式を表示すると
グラフにR-2乗値を表示するにチェックを入れる。
(b) データ分析ツールを用いる方法
回帰式を求めたあとは、その制度を検証する必要がある。
近似曲線だけでは、不十分。
その場合は、データ分析ツールを使用する。
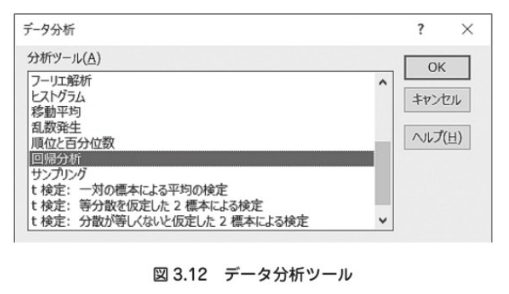
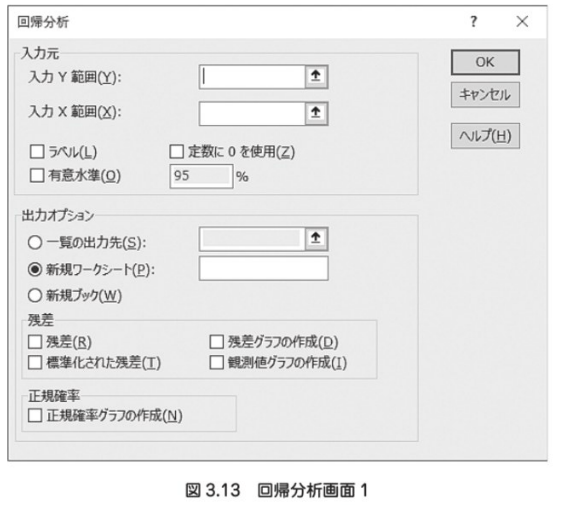
・重相関R
1行下に出てくる重決定R2の正の平方根である。
・重決定R2
(a)近似曲線を追加する方法で出てきた決定係数のこと。
回帰式の当てはまりの良さを表す指標である。
決定係数の方が使われることが多い。
決定係数の値から重相関の値を計算できるため、重決定よりも決定係数の方が重要である。
・補正R2
自由度修正済み決定係数のこと。
自由度とは、データの数から説明変数の数を引いたものである。
回帰分析において、無関係な説明変数であっても、数を増やせば決定係数は上がる。
この影響を排除した当てはまりの指標が、自由度修正済み決定係数である。
・標準誤差
回帰分析において、誤差のバラつきを表すのが、標準誤差である。
標準誤差が小さいほど、分析の精度が高く、逆に大きいほど精度が低いと言える。
・観測数
データの数である。
すべての説明変数が無意味かどうかを確認する。
すべての説明変数の係数が0であるという帰無仮説を立てて、有意F値が十分に小さければ、この帰無仮説は棄却される。
有意F値が0に近いことをもって、全ての説明変数が無意味とは言えないことを確認する。
・係数
説明変数が増えた場合、目的変数にどの程度影響を与えるかを示す。
・標準誤差
回帰分析における誤差のバラつきを表す。
ただし、回帰統計表の標準誤差が回帰分析全体の精度を表すのに対して、ここでの標準誤差は、各説明変数に関する係数のバラ好きを表す。
標準誤差が小さいほど、分析の精度が高く、逆に大きいほど、精度が低いと言える。
・t値
t値から確認できることは、P値で確認ができる上、P値の方が使いやすいため、ここでは説明は省略する。
・P値
説明変数ごとのt値やP値は、その説明変数の係数が0である(説明変数の効果はない)という帰無仮説を棄却できるか否かを確定するための指標である。
自由度を考慮したt検定におけるP値が計算されるため、その値が任意の有意水準よりも小さければ、帰無仮説は棄却される。
その説明変数の係数は、0とは言えない(効果がないとは言えない)となる。
・下限95%/上限95%
説明変数の係数の信頼区間の下限値と上限値で、係数がありそうな範囲を示す。
(4) 回帰式の精度を確認する
回帰式を求めたら、その回帰式が正しいかどうか検証する必要がある。
決定係数が低い場合や、多重共線性の問題が存在するため。
最も簡単な精度確認方法は、決定係数または、自由度修正済み決定係数を確認することである。
相関係数と同じで、値あgいくつ以上になれば良いなどの明確な指標はないが、
0に近いほど回帰式の当てはまりは悪いと言える。
ただし、決定係数がある程度高くても、それだけで回帰式が最適とは断定できない。
説明変数を増やせば、その変数が無関係であっても、決定係数が高くなるため。
次に確認すべきは、説明変数ごとのP値である。
P値が任意の有意水準で棄却域に入る場合、その変数を覗いた上で、再度回帰分析をやり直すことも選択肢となる。
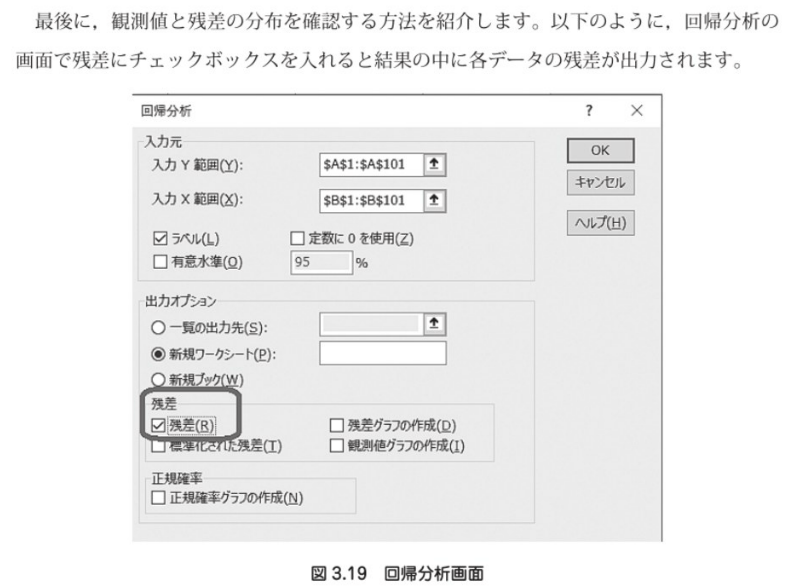
(5) 予測する
回帰分析を行う目的として、統計的検定を踏まえて、説明変数と目的変数の関係を客観的に評価することが挙げられる。
さらに、回帰式を用いて、予測を粉うことが挙げられる。
今回の例では、部屋の面積から、おおよその家賃が予測できる。
他の例では、気温とアイスの売上の関係を回帰式で定量的に表せば、翌日の予想気温からアイスの売上を予測できる。
予測の際には、内挿と外挿に注意が必要である。
内挿とは、回帰式を求めた範囲内(説明変数の最小値と最大値の間)で予測を行うことを言う。
例えば、今回の説明変数に用いた部屋の実データは、最小値9.6、最大値107.6であった。
逆に、回帰式を求めるのに使用した説明変数の範囲を超える値(9.6未満、107.6以上)を予測に用いることを外挿と呼ぶ。
外挿の場合でも、計算によって何らかの結果を得られるが、回帰式が実測値のない範囲でも同様の結果となるため、
データの裏付けがない予測値と成る。
3.3 重回帰分析
2種類以上の変数を説明変数とする回帰分析を重回帰分析と呼ぶ。
単回帰分析では、節目変数は1つのみで、説明変数と目的変数の間は、直線的な関係(線形)が前提であった。
重回帰分析では、各説明変数と目的変数がそれぞれ直線的な関係にあることを前提としている。
重回帰分析では、説明変数が2つの場合に当てはまるのは、平面と成る。
最も当てはまりの良いところを探すにあたっては、コスト(残差)の二重和を最小化するのが鉄則である。
3.3.1 重回帰分析のステップ
サンプルデータ5(回帰分析)
重回帰分析シートを使用する。
3.2.2 係数の大小について
各説明変数の係数の絶対値を比べてみると、物件の階数の0.34が最も大きな値となる。
物件の階数が家賃に与える異教が、その他の説明変数よりも大きいことを意味すると見ることができる。
だが、実際には、係数の大小と目的変数に与える影響の大小は、必ずしも一致しない。
それは、階数が1~9という値に対して、部屋の面積が10~108と異なることが原因となる。
標準化を全ての説明変数について、行い、各説明変数のデータ範囲を0から1に揃えた上で、
重回帰分析を行えば、係数の大小が目的変数に与える影響の大小が一致するようになる。
3.2.3 多重共線性
複数の説明変数を用いる重回帰分析において、説明変数同士に強い相関がある場合には、
正しい結果が得られない。
これを多重共線性と呼ぶ。
この場合、強い相関関係がある説明変数のどちらかを削除して、重回帰分析を行うなど対応が必要となる。
例えば、説明変数Aと説明変数Bの間に強い相関がある場合、それぞれの説明変数と目的変数の相関係数を確認して、
相関係数が高い方の説明変数を残す。(目的変数との相関係数が低い説明変数は削除する)