データ分析と確率は、切り離せない関係にある。
サイコロの目のように不確定である。
1.1 2種類の統計学
統計学は大別して2種類ある。
記述統計学
推測統計学
記述統計学とは、統計量やグラフ、表などを用いて、データの特徴や傾向を把握するもの。
代表例は、国勢調査である。
推測統計学とは、データの一部からデータ全体の状況等の未知のデータを推測するもの。
推定・検定が中心と成る。
統計学では、データ全体のことを母集団と呼ぶ。その中から取り出された一部分のデータのことを標本と呼ぶ。
母集団が大きくなればなるほど、母集団に含まれる全データを観察することは難しくなる。
そうした中では、推測統計学の重要性が増す。
データの規模に関わらず、難点なのは、標本抽出である。つまりは母集団の中からどのようにして、一部分のデータを取り出すかである。
母集団の中から、偏りの有るデータを取り出してしまうと、そこから推測される母集団全体も偏り不正確と成る。
標本抽出には、偏りが出ないようにランダムにサンプリングすることが求められる。
1.2 確率変数
推測統計学に欠かせないのが、確率である。
1.2.1 確率変数とは
確率を伴う不確実な値のことを、確率変数と呼ぶ。
例えば、サイコロの目などは確率変数である。
不確実な値であり、確率変数と言える。
テストの点数や身長など、現実の値は、確率変数ではない。
1.2.2 確率変数の種類
確率変数には、2種類ある。
離散型確率変数
連続型確率変数
(1) 離散型確率変数
離散型確率変数とは、不連続で飛び飛びの値を取り、隣り合う数字の間に値が存在しない確率変数のこと。
例えば、サイコロの目、メールの件数などが挙げられる。
(2) 連続型確率変数
連続型確率変数は、連続的な値を取る確率変数である。
例えば、温度や長さなどが挙げられる。
1.5cmや1.07cmなど無数の値が連続して来る可能性がある。
1.2.3 確率分布
確率分布とは、確率変数の実現値とその確率で示す分布のこと。
確率変数の実現値とは、確率変数が取り得る値のことで、サイコロの例では、1~6のことを指す。
サイコロの確率分布表では、確率変数の実現値とその確率を対応関係表にしたものである。
1.2.4 確率分布をグラフにしてみる
(1) 離散型確率変数の確率分布グラフ
縦軸を確率、横軸を確率変数としてグラフにする。
相対度数とは、その度数が全体に占める割合のことで、下記の式で求めることができる。
相対度数 = 各階級のデータ数/全データ数
相対度数とは、その度数が実現する確率であると言い換えることができる。
相対度数を確率とみなした表が、確率分布表である。
・確率分布グラフとヒストグラム
・確率と相対度数
・確率変数と階級値
上記のように対応関係がある。
(2) 連続型確率変数の確率分布グラフ
連続型確率変数は、確率変数の取り得る値が、連続的になっている。
そのため、確率変数の実現値とその確率の対応関係を文字にすることが困難である。
よって、確率分布表を正確に書くことが出来ない。
ヒストグラムは、連続型確率変数、無限に存在する確率変数の中から一部分だけを
取り出し、あたかも離散型確率変数のように扱うことで、その確率分布をグラフにできる。
極限まで細かくすると、グラフはやがて曲線に成る。
連続した確率分布、連続型確率分布のグラフである。
グラフの横軸は、離散型と同じく、確率変数である。
縦軸は、隔離密度と成る。
よって、連続型確率変数の確率分布グラフを確率密度関数とも呼ぶ。
連続型確率分布の場合、確率とは、確率変数がある特定の区間に入る確率のことを言う。
確率密度とは、その確率を当該区間の大きさで割ったものと言える。
確率密度でいうと、確率とは、面積で表されるとなる。
1.3 正規分布と標準正規分布
1.3.1 正規分布
連続型確率分布には、いくつか種類がある。
その中で基本となるのが、正規分布である。
正規分布は、自然界や人間社会でもよく見られる。
例えば、身長の分布グラフは、正規分布に成る。
このような場合、身長は、正規分布に従うと言う。
正規分布のグラフには、下記の特徴がある。
(1) 平均(μ;ミュー)を中心として左右対称
正規分布のグラフは、平均で折り返すとぴったり重なる。
左右対称のシンメトリーの形を取る。
・平均値でグラフは、頂点を取り、両側に行くほど低くなる。
・平均値と中央値、最頻値は、一致する。
・平均よりxだけ大きい値を取る確率と、平均よりxだけ小さい値を取る確率は、
等しい。
(2) 平均と標準偏差(σ;シグマ)が正規分布の形を決める
正規分布グラフの高さや横幅は、平均と標準の値によって変わる。
・平均がグラフの位置を決める正規分布は、左右に移動させれば重なる。
・標準偏差が広がりを決めるグラフに、小さければ狭いグラフに成る。
平均=0,標準偏差=8の正規分布グラフは、少し幅が広がったグラフとなる。
(3) どんな正規分布でも、一定の範囲に収まる確率が決まっている。
正規分布のグラフであれば、どんな形であっても、下記を満たす。つまり平均や標準偏差に関係なく。
・平均値±標準偏差σの範囲に全体の約68.3%が含まれる。
・平均値±標準偏差σ✕2の範囲に全体の約95.4%が含まれる。
・平均値±標準偏差σ✕3の範囲に全体の約99.7%が含まれる。
例えば、170 cmの平均身長で、標準偏差が5cmだったとする。
身長は、165cm~175cmに含まれることになる。
1.3.2 標準正規分布
正規分布の中でも、特に平均値が0,標準偏差が1のものを標準正規分布と呼ぶ。
平均μ、標準偏差σの正規分布に従う確率変数Xについて
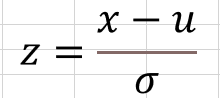
Zは、平均が0,標準偏差が1の標準正規分布に従う確率変数となる。
上辺のXーμは、元の正規分布を横にスライドさせることで、平均をゼロの正規分布に変換している。
上辺をσで割ることで、スライドさせた正規分布の標準偏差を1に変換している。
こうすることで、どんな正規分布でも標準正規分布に変換することができる。
これを標準化、または、基準化と呼ぶ。
標準化を行うメリットの一つに、異なる正規分布に従う2つの確率変数を比較できることが挙げられる。
点数だけを比べると数学の方が高いが、それぞれの科目の平均点と比べようとすると平均点も標準偏差も
異なるために、単純比較することができない。
このような場合に、標準化を行うことは有効である。
標準化すると、どちらも同じ標準正規分布に従った状態での相対的な関係を図ることができる。
1.3.3 標準正規分布と確率
標準正規分布において、横軸上で任意の値を指定すると、確率変数がその値より大きいまたは、小さい
確率を求めることができる。
任意の値ごとの確率は、任意の値とそれに対応する確率を表にした標準正規分布表から
読み取ることもできるが、Excel関数から読み取る手法もある。
NORM.S.DIST関数
標準正規分布に従う確率変数が、入力された値よりも小さい確率を求めることができる。下側確率と呼ぶ。
=NORM.S.DIST(1.645,TRUE)
出力値 0.950015094
確率変数が1.645よりも小さい確率は95%であることが確認できる。
確率変数が任意の値よりも大きくなる確率を求める場合には、NORM.S.DIST関数で求めた数字を1から引く
上側確率と呼ぶ。
下側確率を満たす確率変数を求めるには、
NORM.S.INVを使う。
=NORM.S.INV(0.95)
出力値 1.644853627
確率変数が1.645よりも小さい確率は、95%だと確認できたが、ここでは、その逆でも求められるということ。
1.4 様々な確率分布
▼t分布

▼カイ二乗分布
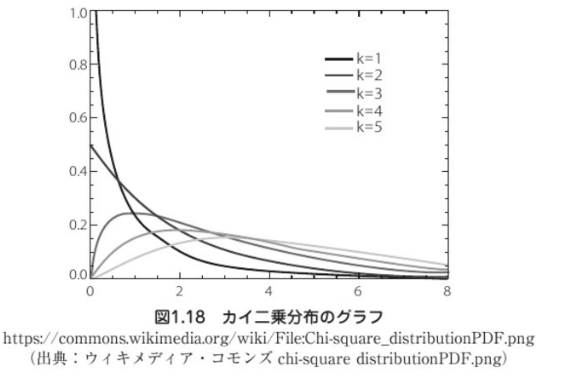
t分布のvおよびカイ二乗分布のkは、自由度を示す。
本講座では、自由度については、データの数から1を引いた値でグラフの形状に影響を与えるものくらいに
理解すれば良い。
基本的には、データの数が多いほど、自由度は大きくなる。
自由度が上がると、t分布も、カイ二乗分布も、グラフの形状が正規分布のグラフに近づいていく。
t分布は、自由度が小さい時から、比較的正規分布に近いグラフの形をしている。
カイ二乗分布は、それほどでもないが、自由度20の場合は、かなり正規分布に近づいていく。
自由度が100になると見た目は正規分布のようになる。