観測対象のデータを分析し、そこから何らかの未知の数字を導き出す、推定や推定値の確かさを判断する検定は、
データ分析の実務に置いて、非常によく使われる手法である。
2.1 推定
一部分のデータから、データ全体の平均や分散などを求めることを、推定という。
例えば、大学生の平均身長を算出したい場合、大学生全員の身長を測る。出来ない場合は、サンプルを集める。
サンプルから全体の平均や分散などを求めるのが推定である。
2.1.1 点推定と区間推定
推定の分類
推定には、点推定と区間推定に大別できる。
点推定とは、推定値として、1つの値を求めるもの。
区間推定とは、推定値を区間で求めるもの。
推定値は、未知の値であり、正解を知ることは出来ない。
区間内には、値が入っているだろうと推定するの区間推定である。
母集団の平均と分散の推定における点推定と区間推定の方法
正規分布に従う母集団のことを正規母集団と呼ぶ。
(1) 点推定
① 母集団の平均(母平均)の点推定
母平均の点推定は、標本の平均から点推定される母平均の値(母平均の点推定量、
または、点推定値)は、標本平均と一致する。
点推定される母平均=標本平均
② 母集団の分散(母分散)の点推定
母分散の点推定は、標本分散をサンプル数で除して求める。

(2) 区間推定
推定値が含まれるであろう区間のことを信頼区間と呼ぶ。
推定値のため、信頼区間の中に現れない可能性もある。
推定値が信頼区間に現れない確率をaとすると、推定値が信頼区間に現れる確率を
(1-a)と表すことができる。
(1-a)を信頼係数と呼ぶ。
標準正規分布
斜線部分の面積が信頼係数(1-a)である。
信頼係数が大きくなるほど、斜線部分の面積は大きくなる。
これは、推定値が信頼区間に現れない確率aが下がることを意味する。
この面積=信頼係数を大きくし過ぎると、信頼区間が広くなり過ぎる。
これは、推定値の範囲が広くなることを意味しており、広すぎる推定値は精度が低くなってしまい意味がない。
よって、信頼係数は、95%、99%を使うことが統計学的な慣例となっている。
① 母集団の平均(母平均)の区間推定
母平均を区間推定する場合、母分散の値が既知であるか、未知であるか分けて考える必要がある。

これを満たす上限、下限は、Excel関数
NORM.S.INV
を用いることで簡単に求めることができる。
よって、信頼係数が95%、つまりaが5%であれば、aに0.55を代入して、
信頼区間の下限値が-1.960、上限値が1.960だとわかる。
母平均について、整理すると、下記の如く成る。


b)母分散が未知の場合
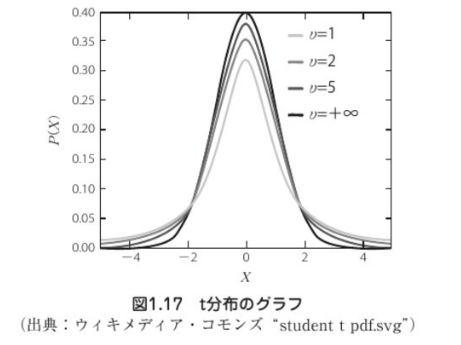
母分散が未知である場合、a)と同じ手順で区間推定を行おうとすると、標準化された標本平均を求めることが出来ず、
推定をすすめることができない。(母分散が未知であれば、母標準偏差も未知であるため)
そのため、標本統計量と呼ばれる下記の値を用いることになる。
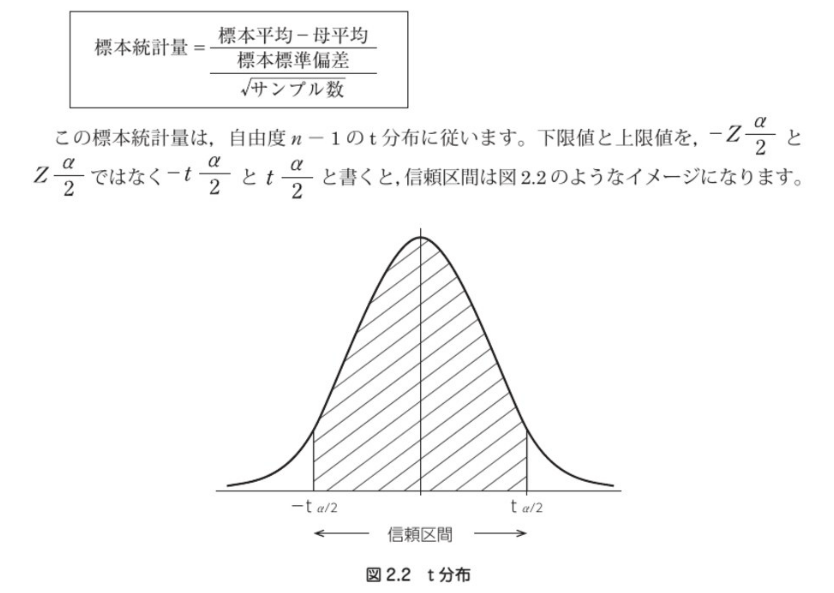
t分布に従う標本統計量を使う点がa)と異なる。

Excel関数
T.INV.2T

② 母集団の分散(母分散)の区間推定
母分散の区間推定の基本的な考え方は、母平均の区間推定とほど同様である。
違いは、標準化された標本平均や標本統計量の代わりに

を使うことである。
使う確率分布が異なるだけ。
母平均の区間推定においては、
母分散が既知であれば、標準正規分布を使う。
母分散が未知であれば、t分布を使う。
母分数では、カイ二乗分布を使う。

エクセル関数
CHISQ.INV.RT
2.2 検定
データはバラつきがつきものである。
データのばらつきを考慮した上で客観的な判断を行う必要がある。
この統計的な判断方法を検定と呼ぶ。
2.2.1 検定の考え方
検定においては、有るデータに対して仮設を立て、その仮設は成り立つか?を考える。
この判断には、統計的な確率計算を用いて、データを観察し、その仮設が観察される確率を計算する。
確率が極稀にしか起こらない場合、仮設が間違っている・下越が成り立たない
と判断する。
これが検定の基本的な考え方である。
2.2.2 検定の手順
(1) 帰無仮説を立てる
(2) 対立仮説を立てる
(3) 有意水準を決める
(4) 棄却域を求める
(5) 検定統計量を計算する
(6) 有意性を判定して、結論を出す
(1) 帰無仮説を立てる
帰無仮説とは、検定の始めに立てる仮設のことである。
帰無仮説の例としては、母平均はXXであるや、グループAとグループBの平均に差がないなど
(2) 対立仮説を立てる
帰無仮説に対立する仮設のことである。
対立する仮設のため、帰無仮説を否定するような内容と成ることがほとんどである。
検定では、立てた仮設が正しいかを考える。
立てた仮設=帰無仮説が正しくないと判断された場合に採用されるのが、対立仮説である。
例えば、帰無仮説が、母平均はXXであるとすれば、これに対立する仮設は、
・母平均はXXではない 両側検定
・母平均はXXより低い OR 母平均はXXより高い 片側検定
(3) 有意水準を決める
極稀にしか起こらない確率とは、最初に定めておく必要がある。
この確率のことを、有意水準と呼び、αで表す。
αの大きさについては、決まりはないが、
α=0.05 α=0.01とするのが統計学的な慣例となっている。
α=0.05 は、5%以下の確率で発生し得る事象となり、最も一般的な極稀の値となる。
(4) 棄却域を求める
棄却域は、有意水準αによって、与えられる。
検定統計量が棄却域に入っていれば、帰無仮説が棄却(帰無仮説は正しくないと判定する)領域です。
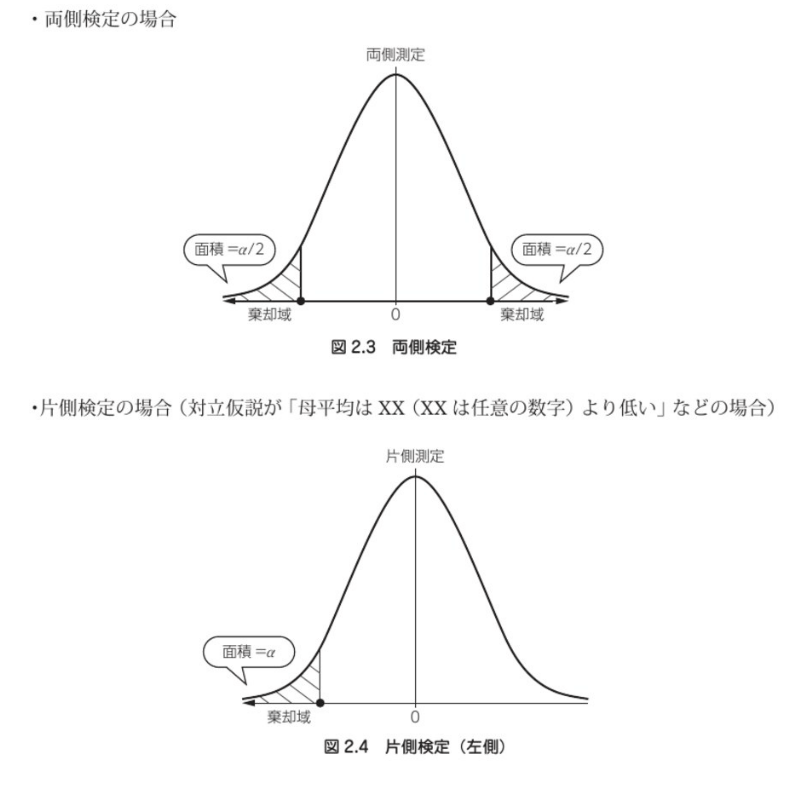
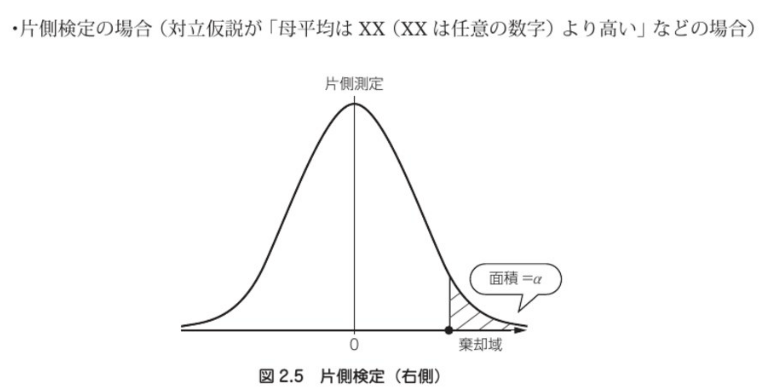
横軸に確率変数、縦軸に確率密度を執った場合、確率変数がある一定区間の値を取る確率が面積で表される。
有意水準よりも小さくなるような確率変数の範囲のことを、棄却域と呼ぶ。
検定に用いる、棄却域を求めるための確率分布も、用途によって使い分けをする。
例えば、既知の母分数を用いた母平均の検定を行う場合、標準正規分布を使う。
未知の母分数を用いた母平均の検定であれば、t分布を使う。
棄却域を算出する際、推定の下限値・上限値を求めたExcel関数を使うと便利である。

(5) 検定統計量を計算する
検定統計量とは、仮説検定の基準となる統計量のことである。
検定統計量は、例えば、母平均の推定量などで、三週の方法は、区間推定が参考となる。
(6) 有意性を判定して、結論を出す
検定統計量と、棄却域を求めた確率分布のグラフの横軸の値を照らし合わせ、検定統計量が棄却域に入っているかどうかを調べる。
これを有意性を判定すると呼ぶ。
検定統計量が棄却域に入っている場合は、帰無仮説が誤りとなり、対立仮説が正しいと成る。
検定統計量が棄却域に入っていない場合は、帰無仮説を棄却することは出来ない。
帰無仮説が棄却されないことと、帰無仮説が積極的に採択することは同意ではない。
★★
検定統計量が棄却域に入っていない場合でも、それは、棄却する根拠を得られなかっただけで、帰無仮説が正しいとは言い切れない。
2.2.3 P値
P値をもとに有意性を判定することもできる。
P値とは、図2.6の傾斜部分の面積のこと。
面積=確率を素にして、帰無仮説を棄却するかどうかを判断する。
P値のPha,Probability(確率)の頭文字である。
検定統計量からP値を算出し、それが有意水準として、定めた任意の確率よりも小さければ、帰無仮説が棄却される。
検定統計量が棄却に入ること、とP値が有意水準よりも小さいことは、同じ意味である。
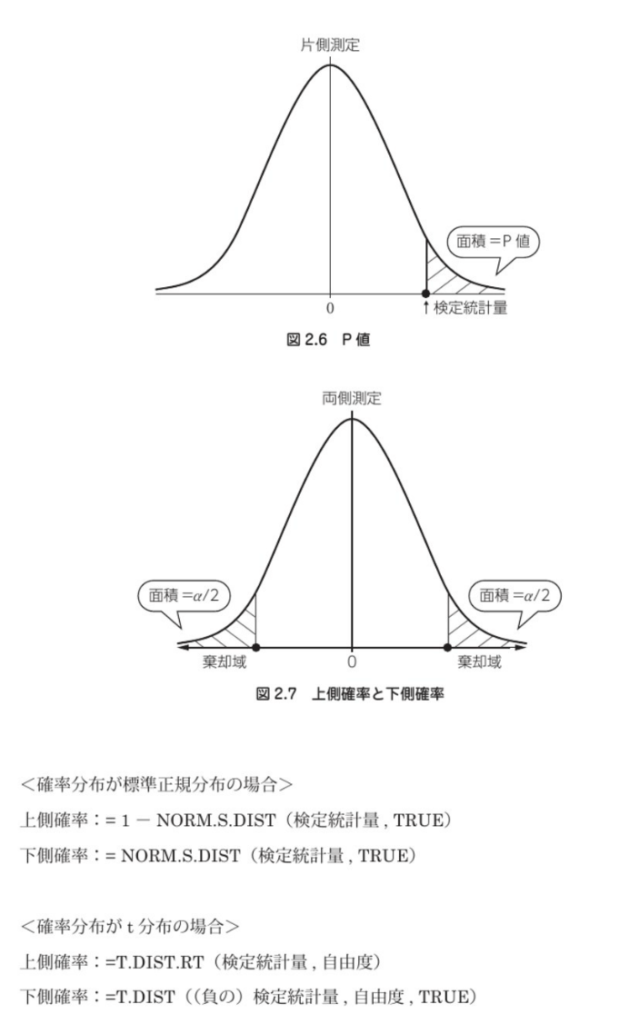
<確率分布がカイ二乗分布の場合>
上側確率 :=CHISQ.DIST.RT(検定統計量,自由度)
下側確率 :=CHISQ.DIST.RT(検定統計量,自由度)
2.2.4 仮説検定(母分数が既知の場合の母平均)
A高校 数学平均点 60 点
標準偏差 5 点
B高校 数学平均点 61 点
標準偏差 5 点
上記の条件の時、B高校の平均点は、A高校に比べて高いと言えるかどうか、検定で確かめてみよう。
(1) 帰無仮説を立てる
帰無仮説:B高校全体の平均点は、60点である。
(2) 対立仮説を立てる
対立仮説:B高校の平均点は60点より高い 片側検定
※検定によって、帰無仮説が棄却された場合、B高校の平均点がA高校よりも高いと結論づけることができる。
(3) 有意水準を決める
有意水準αを決める。
α=0..05 すなわち、5%以下の確率で発生し得る事象を極稀であると定義する。
(4) 棄却域を求める
棄却域をは、有意水準αによって、与えられるが、今回は、(3)の通り5%と決めた。
今回は対立仮説が~より高いとしているので、右辺側検定と成る。

今回知りたいのは、B高校の生徒100人の点数からB高校全体の平均点である。
B高校の標準偏差は、A高校と同じ5点である。
これは、母集団をB高校全体とし、母分散が既知で、母平均を推定することになる。
この推定では、標準正規分布を使う。
用いる確率分布が分かれば、Excel関数から棄却域を求められる。
Excelの任意のセルで
=NORM.S.INV(1-0.05)
を実行する。
今回は片側検定のため、’=NORM.S.INV(1-0.025)とはならない。
出力値 1.644853627
求める検定統計量が出漁値の1.644854よりも大きければ、帰無仮説は棄却される。
(5) 検定統計量を計算する
今回の検定統計量は、B高校全体を母集団とした場合の母平均である。
母分散は、既知のため、検定統計量は下記の式で求めることができる。
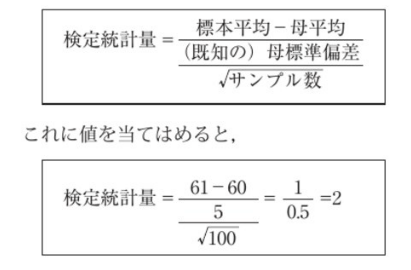
母平均には、A高校平均である60点を入れているが、これは帰無仮説通り、
A高校の平均点とB高校の平均点が等しいとした場合、B高校の点数分布もA高校と同じ分布に成る。
(6) 有意性を判定して結論を出す
帰無仮説は正しくなく、対立仮説が正しいと言える。
すなわち、B高校の平均点は、A高校よりも高い(B高校の平均点は、A高校の平均点60点より高い)と言える。
P値からもこの結論が正しいかを確認する。
P値は、下記のExcel関数で求めることができる。
=1-NORM.S.DIST(2,TRUE)
出力値 0.022750132
P値は、2.28%となる。
有意水準5%(0.05)を下回っているので、
P値からも帰無仮説が、棄却されることが確認できる。
もし、有意水準1%とした場合、棄却域は、2.326以上となる。
2.2.5 仮説検定(母分散が未知の場合の母平均)
母分散が未知である場合の検定手順の確認
例)A高校とB高校のテストの点数
B高校の標準偏差が未知(A高校と等しいかは不明である)
観察した100人の生徒の点数の標準偏差は7であった。
(1)帰無仮説と’(2)対立仮説は、母分散が基地の場合の検定と同じものとする。
(3)有意水準も同じく5%とする。
帰無仮説:B高校全体の平均点は60点でる
対立仮説:B高校の平均点は60点より高い
(4) 棄却域を求める
用いる確率分布はt分布とする。
棄却域を求めるには、Excel関数を使う。
=T.INV(1-0.05,99)
出力値 1.660391156
間作した100人サンプルのため、自由度は99となる(100-1)
結果の出力値は、1.660
検定統計量がこの値よりも大きければ、帰無仮説は棄却される。
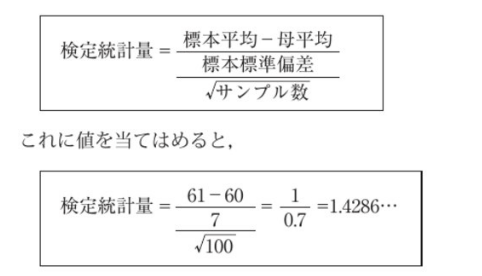
(5) 検定統計量を計算する
B高校全体を母集団とし、母分散が未知の母平均を求めたいので、検定統計量は下記の式で求められる。

(6) 有意性を判定して結論を出す
(5)で計算した検定統計量は、1.4286
(4)で求めた棄却域(>1.660)以下のため、帰無仮説は棄却されず、
B高校の平均点は、A高校より高いとは言えないことがわかる。